Thu, 13 Nov 2025,arXiv:2511.10647


引言:三维视觉感知的”大道至简”
DA3实现了视觉三维感知领域的重要突破,它能从任意数量、任意视角的视觉输入中,恢复出空间一致的三维几何结构,无需复杂的多任务学习,达到从任意数量的图像中重建视觉空间,实现了媲美人类的空间感知。
DA3创新点概览
- 追求最小建模:
- 单一骨干网络:只需要一个简单的 ViT 预训练骨干网络就行了,不需要专门设计的架构。
- 追求 3D视觉任务 的通用模型:
- 统一表示方法:只需要一个用 深度-光线 表示训练,无需复杂的 3D 任务。
- 统一框架设计:单目深度估计、运动结构重建(SfM)、多视图立体(MVS)、即时定位与地图构建(SLAM)。
- 数据驱动:追求大规模数据集的高效利用:
- 多元化数据:充分利用海量且多样化的训练数据。包括真实世界深度相机采集的数据、通过三维重建技术生成的数据、完全由计算机合成的数据。
- 多样化数据的处理。相对深度与真实深度的对齐,天空区域处理、置信度等。
- 所有模型均在公共学术数据集上训练。
- 追求 3D视觉任务模型的多数据自适应输入:
- 支持多种输入模式:单张图像、场景的多视角图像、视频流。可选相机参数。
- 追求针对多样化数据的模型训练方式:
- 师生范式,统一各种不同的训练数据。
- 领域新地位,建立该视觉几何领域的新测试基准:涵盖相机姿态估计、任意视图几何和视觉渲染。
性能提升:
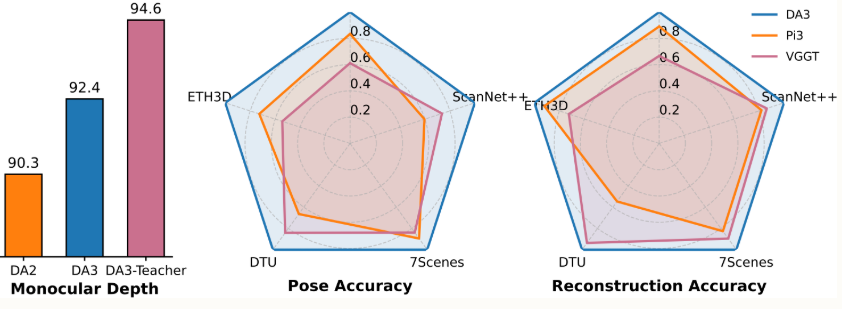
测试基准-五边形战士
就是这样的方法,在新测试基准的所有 10 项任务中都取得了新的 SOTA 成绩。 尽管使用更简单的架构,在单目深度估计方面优于 Deepth Anything V2;在最新提交中,相机姿态精度方面比之前的 SOTA VGGT 平均提高了 44.3%;在几何精度方面提高了 25.1%。
理解三维空间
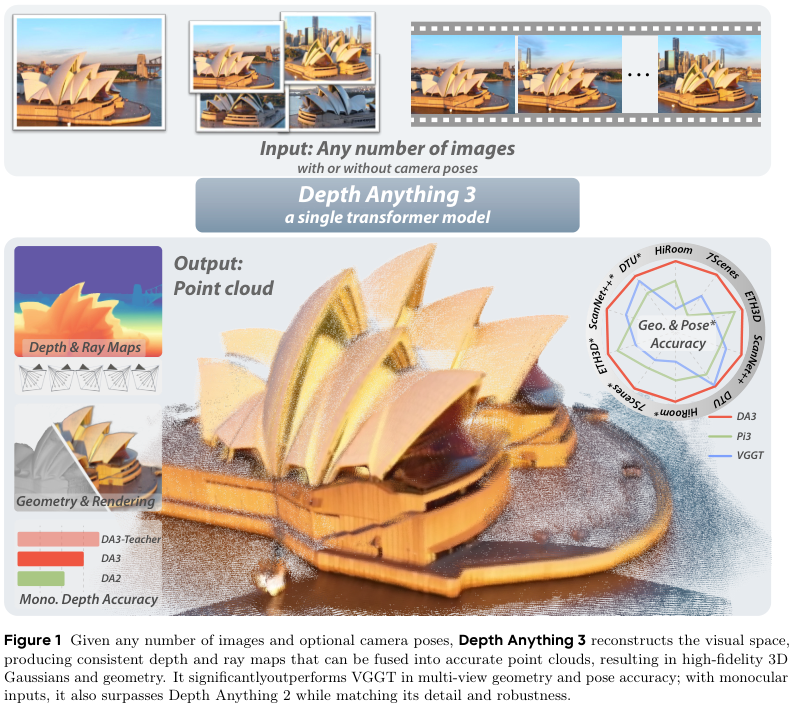
人类天生具备从眼睛看到的画面中理解空间的能力,这种能力是机器人导航、混合现实等前沿科技应用的核心。 为了在机器上复现这种能力,计算机视觉领域衍生出一系列看似不同却又很相关的任务, 比如DA3中,主要包含:
- 从 单张图片 估算距离远近的单目深度估计(Monocular Depth Estimation),
- 利用 多个视角的图像 生成三维模型的多视图立体视觉(Multi-View Stereo),
- 从 移动的画面 中恢复物体结构的运动恢复结构(Structure from Motion),
- 让机器在未知环境中实时定位并构建地图的同时定位与地图构建(Simultaneous Localization and Mapping)。
这些任务的本质目标都是理解三维空间,区别常常只在于输入的是一张图、多张图还是一段视频。
过去,主流的研究范式是为每一个细分任务设计一套高度专门化的模型和算法。这种模式虽然在特定场景下效果不错,却导致了技术上的壁垒和资源上的浪费。 近期虽有研究尝试构建统一模型来处理多个任务,但它们往往依赖于复杂且定制化的架构,需要从零开始进行联合优化练,这使得它们难以有效利用今天已经非常强大的大规模预训练模型的知识。 为了实现这个目标,DA3摒弃了繁杂的架构工程,采用了一种极简的建模策略。一个最小化的预测目标集合,就能完整地描述三维几何。通过一个普通的、未经特殊改造的 Transformer 模型,足以胜任这个统一建模。
一个极简模型
以往3D视觉模型通常依赖复杂定制的架构,需要从零开始进行跨任务联合优化,因此无法有效利用大规模预训练模型。
DA3巧妙地将所有三维几何重建任务,统一表述为一个简单的密集预测问题。具体来说,给定输入图像,模型的核心任务就是输出与之对应的深度图和射线图(射线表示进行任意视角深度和姿态联合)。深度图告诉我们每个像素点的远近,而射线图则记录了每个像素点在空间中的方向和原点。实现这一目标的架构以标准的预训练ViT作为骨干网络,充分利用其特征提取能力。
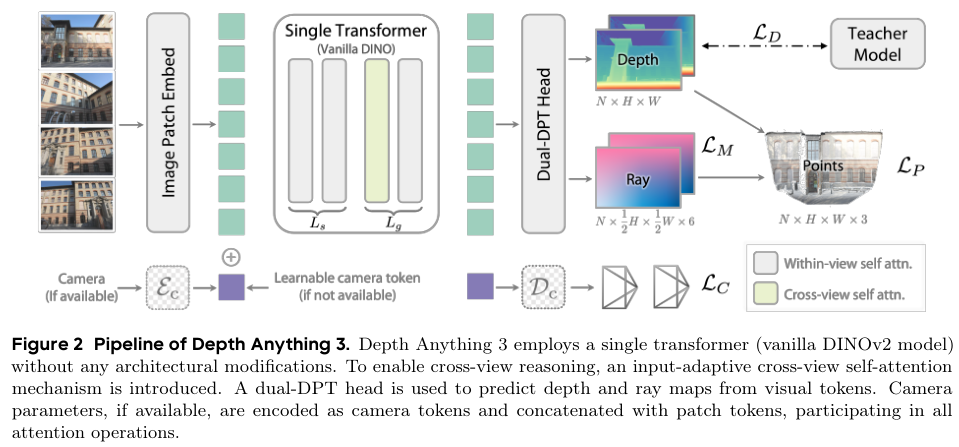
实现这一目标的架构出奇地简洁。它的主干网络是一个标准的、已在海量图像数据上预训练过的视觉Transformer,例如DINOv2。这使得DA3可以直接站在巨人的肩膀上,继承其强大的图像特征提取能力。
多样化数据
处理任意数量的视图是这类统一模型的关键难点。 DA3引入了一个核心创新:输入自适应的跨视图自注意力机制(input-adaptive cross-view self-attention mechanism)。 动态token重排:这个机制并不需要修改Transformer的底层结构,而是在模型进行前向传播时,在特定的网络层动态地重新排列token,让来自所有输入视图的信息能够高效地交流和融合,实现空间的一致。
将 Transformer 划分为大小为 ${L}{s}$ 和 ${L}{g}$ 的两组模块。前 ${L}{s}$ 层在每张图像内部应用自注意力,而后续 ${L}{g}$ 层则在跨视图和视图内注意力之间交替执行,通过张量重排序在所有 token 上联合运算。
分层处理策略:具体实现上,DA3将Transformer的网络层分为前后两组,比如前三分之二的层专注于在单张图像内部处理信息,而后三分之一的层则在跨视图信息交互和视图内信息处理之间交替进行。 输入自适应性:这种设计是输入自适应的,当输入只有一张图像时,模型会自动退化为标准的单目深度估计模式,不会产生任何额外的计算开销。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def process_attention(self, x, block, attn_type="global", pos=None, attn_mask=None):
b, s, n = x.shape[:3] # batch, seq(views), num_patches
if attn_type == "local":
x = rearrange(x, "b s n c -> (b s) n c")
if pos is not None:
pos = rearrange(pos, "b s n c -> (b s) n c")
elif attn_type == "global":
x = rearrange(x, "b s n c -> b (s n) c")
if pos is not None:
pos = rearrange(pos, "b s n c -> b (s n) c")
# ...
x = block(x, pos=pos, attn_mask=attn_mask)
# ...
return x
def _get_intermediate_layers_not_chunked(self, x, n=1, export_feat_layers=[], **kwargs):
# ...
if self.alt_start != -1 and i >= self.alt_start and i % 2 == 1:
x = self.process_attention(
x, blk, "global", pos=g_pos, attn_mask=kwargs.get("attn_mask", None)
)
else:
x = self.process_attention(x, blk, "local", pos=l_pos)
local_x = x
# ...
以上代码可以看出,模型在”global”和”local”注意力之间交替进行: “global”注意力:将所有视图的token展平,实现跨视图的信息交流。 “local”注意力:在每个视图内部独立处理信息。 “alt_start” 参数:被设置为总层数的三分之二处。
dual-DPT: 在预测阶段,DA3提出了一个新的双DPT(Dense Prediction Transformer)头,它接收来自主干网络的同一组特征图,然后通过使用不同融合参数的两套分支,同时输出最终的深度图和射线图。 这种设计鼓励两个预测任务之间进行深层的信息共享,同时又避免了产生冗余的中间表示,既高效又精准。
DPT 头提供经典深度预测,可选天空分割:
- 多尺度融合:4层自顶向下特征融合。
- 天空检测:专用天空头处理无限深度区域。对天空区域的特殊处理确保鲁棒深度估计。
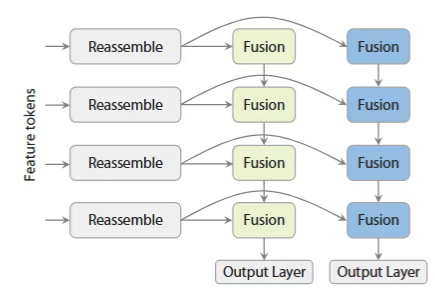
dual-DPT
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# ...
# Main head
self.scratch.output_conv2 = nn.Sequential(
nn.Conv2d(head_features_1 // 2, head_features_2, kernel_size=3, stride=1, padding=1),
*ln_seq,
nn.ReLU(inplace=True),
nn.Conv2d(head_features_2, output_dim, kernel_size=1, stride=1, padding=0),
)
# Sky head (fixed 1 channel)
if self.use_sky_head:
self.scratch.sky_output_conv2 = nn.Sequential(
nn.Conv2d(
head_features_1 // 2, head_features_2, kernel_size=3, stride=1, padding=1
),
*ln_seq,
nn.ReLU(inplace=True),
nn.Conv2d(head_features_2, 1, kernel_size=1, stride=1, padding=0),
)
# ...
def _fuse(self, feats: List[torch.Tensor]) -> torch.Tensor:
"""
4-layer top-down fusion, returns finest scale features (after fusion, before neck1).
"""
l1, l2, l3, l4 = feats
l1_rn = self.scratch.layer1_rn(l1)
l2_rn = self.scratch.layer2_rn(l2)
l3_rn = self.scratch.layer3_rn(l3)
l4_rn = self.scratch.layer4_rn(l4)
# 4 -> 3 -> 2 -> 1
out = self.scratch.refinenet4(l4_rn, size=l3_rn.shape[2:])
out = self.scratch.refinenet3(out, l3_rn, size=l2_rn.shape[2:])
out = self.scratch.refinenet2(out, l2_rn, size=l1_rn.shape[2:])
out = self.scratch.refinenet1(out, l1_rn)
return out
相机编码器: 为了增加模型的灵活性,使其能适应各种真实场景,DA3还设计了一个可选的轻量级的相机编码器。 如果输入图像的相机位姿(位置、朝向、焦距等)是已知的,这些信息就可以通过这个编码器整合到模型中,为几何重建提供明确的约束。
- 内参:
\(K = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix}\)
其中 $f_x$, $f_y$ 表示相机在水平方向和垂直方向上的焦距,单位为像素;$c_x$, $c_y$ 是图像主点,通常位于图像中心;对于图像大小为 $W \times H$,常设 $c_x = W / 2$,$c_y = H / 2$。
- 视场角: 焦距与视场角之间的关系来源于几何三角函数,可表达为: \(\text{FOV}_x = 2 \cdot \arctan\left(\frac{W}{2 f_x}\right)\), \(\text{FOV}_y = 2 \cdot \arctan\left(\frac{H}{2 f_y}\right)\) 其中 $\text{FOV}_x$, $\text{FOV}_y$表示水平与垂直方向的视场角,单位为弧度。
- 外参: \(E = \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}\) 其中 ( R ):3x3 旋转矩阵,( t ):3x1 平移向量,( P ):1x4 透视向量。
如果位姿未知,模型也能正常工作。这种整体设计,最终形成了一个干净、优雅且具备良好扩展性的架构,能够直接受益于其预训练主干模型的规模效应。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def affine_inverse(A: torch.Tensor):
R = A[..., :3, :3] # ..., 3, 3
T = A[..., :3, 3:] # ..., 3, 1
P = A[..., 3:, :] # ..., 1, 4
return torch.cat([torch.cat([R.mT, -R.mT @ T], dim=-1), P], dim=-2)
def extri_intri_to_pose_encoding(
extrinsics,
intrinsics,
image_size_hw=None,
):
"""Convert camera extrinsics and intrinsics to a compact pose encoding."""
# extrinsics: BxSx3x4
# intrinsics: BxSx3x3
R = extrinsics[:, :, :3, :3] # BxSx3x3
T = extrinsics[:, :, :3, 3] # BxSx3
quat = mat_to_quat(R)
# Note the order of h and w here
H, W = image_size_hw
fov_h = 2 * torch.atan((H / 2) / intrinsics[..., 1, 1])
fov_w = 2 * torch.atan((W / 2) / intrinsics[..., 0, 0])
pose_encoding = torch.cat([T, quat, fov_h[..., None], fov_w[..., None]], dim=-1).float()
return pose_encoding
相机解码器,将学习表示映射回相机参数,从特征表示提供最终参数估计。包括平移向量(3D),旋转四元数(4D),视场参数(2D)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class CameraDec(nn.Module):
def __init__(self, dim_in=1536):
super().__init__()
output_dim = dim_in
self.backbone = nn.Sequential(
nn.Linear(output_dim, output_dim),
nn.ReLU(),
nn.Linear(output_dim, output_dim),
nn.ReLU(),
)
self.fc_t = nn.Linear(output_dim, 3)
self.fc_qvec = nn.Linear(output_dim, 4)
self.fc_fov = nn.Sequential(nn.Linear(output_dim, 2), nn.ReLU())
def forward(self, feat, camera_encoding=None, *args, **kwargs):
B, N = feat.shape[:2]
feat = feat.reshape(B * N, -1)
feat = self.backbone(feat)
out_t = self.fc_t(feat.float()).reshape(B, N, 3)
if camera_encoding is None:
out_qvec = self.fc_qvec(feat.float()).reshape(B, N, 4)
out_fov = self.fc_fov(feat.float()).reshape(B, N, 2)
else:
out_qvec = camera_encoding[..., 3:7]
out_fov = camera_encoding[..., -2:]
pose_enc = torch.cat([out_t, out_qvec, out_fov], dim=-1)
return pose_enc
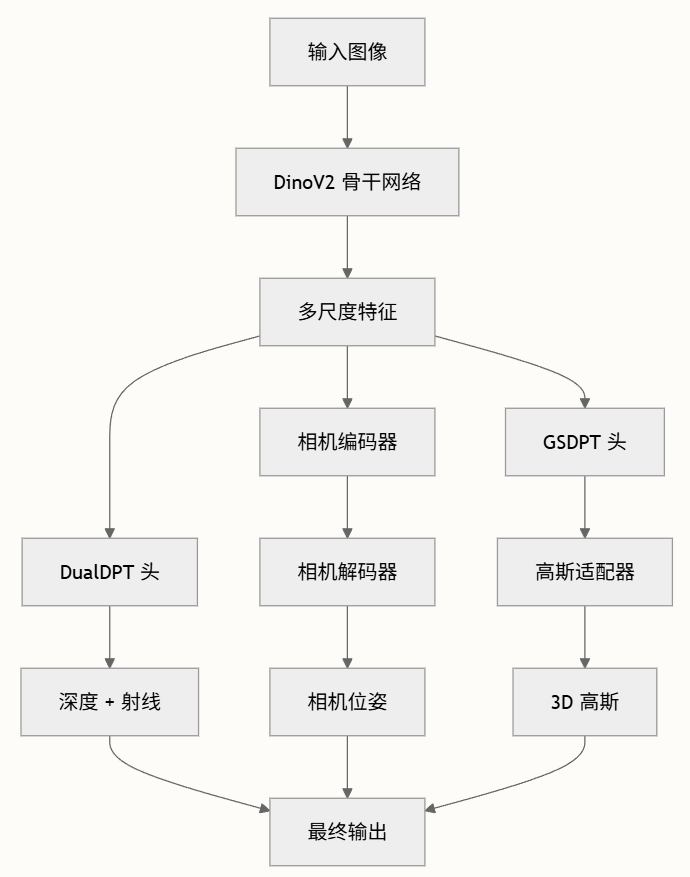
(相机位姿和3D高斯组件基于配置可选)
用深度-射线表示法解构三维空间
深度预测与射线方向估计在计算机视觉中本质上是耦合问题,将深度与射线方向建模为联合表征,同时捕获 3D 场景几何的梯度与方向性。该理论建立了传统深度图与基于射线表征之间的原理性联系,实现了与现代 3D 渲染技术(如 Gaussian Splatting)的无缝集成。
传统方法中,直接预测相机位姿的旋转矩阵(Rotation Matrix)是一个棘手的技术难题。为了绕开这个难题,DA3采用了一种更巧妙的隐式表示方法:用与每个像素点对齐的射线图(Ray Map)来替代直接预测相机位姿。空间中的一条射线可以由它的原点(Origin)和方向(Direction)唯一确定。
对于图像上的每一个像素点,都可以想象有一条光线从相机中心出发,穿过这个像素点,射向三维空间中的某个物体点。这条光线的原点就是相机中心的位置,方向则是从相机中心指向该像素点的向量。
- 射线起点:由外参参数导出的世界坐标系中的相机位置。
- 射线方向:从相机穿过每个像素的归一化向量,通过反投影和相机到世界变换计算。
1
2
3
4
5
6
7
8
9
10
11
12
13
def get_world_rays(coordinates, extrinsics, intrinsics):
# 将图像坐标反投影到相机坐标系,单位向量
directions = unproject(coordinates, torch.ones_like(coordinates[..., 0]), intrinsics)
directions = directions / directions.norm(dim=-1, keepdim=True)
# 转换到世界坐标系
directions = homogenize_vectors(directions)
directions = transform_cam2world(directions, extrinsics)[..., :-1]
# 从外参中提取相机原点
origins = extrinsics[..., :-1, -1].broadcast_to(directions.shape)
return origins, directions
这种表示方法的优势: DA3的模型就为输入图像的每个像素点预测这样一个六维的射线参数(三维原点坐标+三维方向向量),形成一张密集的射线图。同时,模型还预测一张对应的深度图,告诉我们每个像素点代表的物体沿着对应射线方向的距离。 有了深度图和射线图,三维空间的重建就变得异常简单:三维点坐标 = 射线原点 + 深度值 × 射线方向。这个公式用最基础的向量运算,就将二维图像信息还原到三维世界中,并且由于所有像素的射线原点和方向都在一个统一的世界坐标系下,生成的点云自然就是空间一致的。 这种深度-射线表示法构成了一个最小且完备的目标集,它既能精确描述场景的几何结构,又能隐式地编码相机的运动信息,效果优于之前工作所采用的点图(Point Map)或其他更复杂的输出组合。
虽然这个表示法很简洁,但在推理时,如果需要从预测出的密集射线图中反向求解出相机的精确位姿参数(如旋转矩阵、焦距等),计算会比较耗时。为了解决这个实际应用中的不便,DA3额外增加了一个极其轻量级的相机头,它专门处理与每个视图关联的相机camera token,直接预测出相机的内参外参,视场、旋转(以四元数形式)和平移参数。因为每个视图只有一个这样的token,所以增加的计算成本几乎可以忽略不计,却大大方便了下游应用。
老师-学生范式
面对真实世界数据质量参差不齐的问题,DA3 采用了高效的教师-学生范式。
要训练一个能处理各种场景的通用模型,就需要海量且多样化的训练数据。 这些数据来源各异,包括真实世界中用深度相机采集的数据、通过三维重建技术生成的数据,以及完全由计算机合成的数据。 这里存在一个核心矛盾:真实世界的数据虽然宝贵,但质量往往不尽人人意。例如,消费级的深度相机采集的深度图常常充满噪声、存在空洞,或者在物体边缘处非常模糊。 而合成数据虽然可以生成完美、稠密的深度标签,但与真实世界之间始终存在一道次元壁,模型在合成数据上学到的知识可能无法很好地泛化到真实场景。

其中真实世界的深度数据质量可能较差。为了解决这个问题,作者采用了一种受先前工作启发的伪标注策略,使用合成数据训练一个强大的单目深度模型,从而为所有真实世界数据生成密集、高质量的伪深度图。
为了解决这个难题,DA3采用了一种高效的教师-学生范式。 首先,DA3团队构建了一个异常强大的教师模型。这个教师模型只在海量的、高质量的合成数据上进行训练。
事实证明,这种方法非常有效,在不牺牲几何精度的前提下,显著提高了标签的细节和完整性。
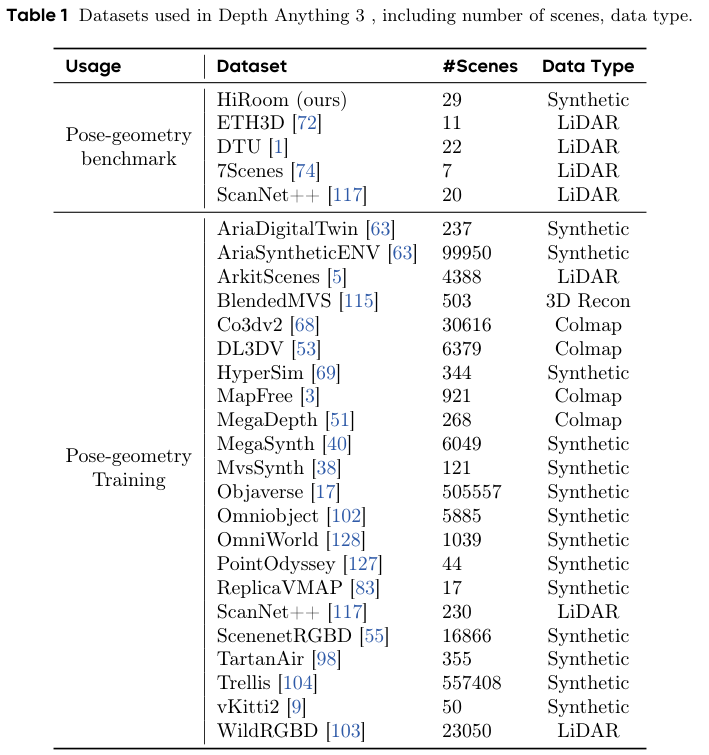
教师模型:
训练数据:
覆盖了室内、室外、以物体为中心以及各种野外场景,确保了教师模型具备了对精细几何细节的深刻理解。包括:Hypersim, TartanAir, IRS, vKITTI2, BlendedMVS, SPRING, MVSSynth, UnrealStereo4K, GTA-SfM, TauAgent, KenBurns, MatrixCity, EDEN, ReplicaGSO, UrbanSyn, PointOdyssey, Structured3D, Objaverse, Trellis, OmniObject。
这个教师模型本身就是一个顶级的单目深度估计模型,其架构与DA3的主框架保持一致,由DINOv2视觉Transformer和DPT解码器组成,没有任何专门的架构修改。
为了解决深度值在近距离区域不敏感的问题,模型预测的是指数深度,这放大了近处物体的区分度。
这个教师模型训练好之后,就成为了一个高质量伪标签的生产工厂。对于所有真实世界的训练数据,无论其原始的深度标签是稀疏的、有噪声的还是完全缺失的,DA3都用这个教师模型去预测一个密集、干净且细节丰富的相对深度图。
深度对齐-尺度一致性: 为了保证几何的准确性,DA3将教师模型生成的相对深度图,与原始数据中的那些稀疏、有噪声真实尺度信息的深度值进行对齐。 这个过程通过一个鲁棒的 RANSAC(随机样本一致性)最小二乘法来完成,使得变换后的预测深度与真实深度之间的平方误差最小。它能自动找到最佳的尺度和平移参数,将相对深度转换到真实的度量空间。这种方法假设预测深度和真实深度之间存在线性关系:真实深度 = 缩放因子 × 预测深度 + 平移参数。
第一个公式表示通过最小二乘法找到最优的缩放因子 $s$ 和平移参数 $t$。第二个公式表示使用优化得到的参数对预测深度图进行变换,得到与真实深度对齐的深度图。
\((\hat{s}, \hat{t}) = \arg\min_{s>0, t} \sum_{p \in \Omega_m} p(s \tilde{\mathbf{D}}_p + t - \mathbf{D}_p)^2\), \(\mathbf{D}_{T \rightarrow M} = \hat{s} \tilde{\mathbf{D}} + \hat{t}\)
其中:
- $\hat{s}$ 和 $\hat{t}$ 分别是优化得到的缩放因子和平移参数。
- $\Omega_m$ 表示用于计算的有效掩码像素区域。
- $\tilde{\mathbf{D}}$ 是教师预测的相对深度图。
- $\mathbf{D}$ 是真实的深度图。
- $\mathbf{D}_{T \rightarrow M}$ 是变换后的深度图。
代码中为寻找一个缩放因子s,使得s * b尽可能接近a。最小二乘问题的目标是最小化:||a - s*b||²,通过求导并令导数为0,可以得到最优解:s = (a·b) / (b·b)。
1
2
3
4
5
6
7
8
9
def least_squares_scale_scalar(
a: torch.Tensor, b: torch.Tensor, eps: float = 1e-12
) -> torch.Tensor:
# a:代表真实深度值(valid_metric_depth); b:代表模型预测的伪深度值(valid_depth)
# ...
# Compute dot products for least squares solution
num = torch.dot(a.reshape(-1), b.reshape(-1))
den = torch.dot(b.reshape(-1), b.reshape(-1)).clamp_min(eps)
return num / den
在训练深度估计模型时,可以使用这个缩放因子来对齐预测值和真实值。
在推理时,可以使用预先计算好的缩放因子将模型的输出转换为真实物理距离。 Metric 系列需要相机内参信息将相对深度预测转换为绝对度量测量。要从DA3METRIC-LARGE的图像获取以米为单位的测距深度,请使用公式metric_depth = focal * net_output / 300.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def apply_metric_scaling(
depth: torch.Tensor, intrinsics: torch.Tensor, scale_factor: float = 300.0
) -> torch.Tensor:
"""
Apply metric scaling to depth based on camera intrinsics.
Args:
depth: Input depth tensor
intrinsics: Camera intrinsics tensor
scale_factor: Scaling factor for metric conversion
Returns:
Scaled depth tensor
"""
focal_length = (intrinsics[:, :, 0, 0] + intrinsics[:, :, 1, 1]) / 2
return depth * (focal_length[:, :, None, None] / scale_factor)
天空区域处理: 天空区域处理确保即使在传统深度线索有限的挑战性户外场景中,深度估计仍保持鲁棒性。
- 天空检测:使用 metric 分支的天空分割,阈值为 0.3。
- 最大深度分配:将天空区域设置为适当的最大深度值。
- 置信度调整:在天空区域分配中保持高置信度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
def _handle_sky_regions(
self,
output: Dict[str, torch.Tensor],
metric_output: Dict[str, torch.Tensor],
sky_depth_def: float = 200.0,
) -> Dict[str, torch.Tensor]:
"""Handle sky regions by setting them to maximum depth."""
non_sky_mask = compute_sky_mask(metric_output.sky, threshold=0.3)
# Compute maximum depth for non-sky regions
# Use sampling to safely compute quantile on large tensors
non_sky_depth = output.depth[non_sky_mask]
if non_sky_depth.numel() > 100000:
idx = torch.randint(0, non_sky_depth.numel(), (100000,), device=non_sky_depth.device)
sampled_depth = non_sky_depth[idx]
else:
sampled_depth = non_sky_depth
non_sky_max = min(torch.quantile(sampled_depth, 0.99), sky_depth_def)
# Set sky regions to maximum depth and high confidence
output.depth, output.depth_conf = set_sky_regions_to_max_depth(
output.depth, output.depth_conf, non_sky_mask, max_depth=non_sky_max
)
return output
def set_sky_regions_to_max_depth(
depth: torch.Tensor,
depth_conf: torch.Tensor,
non_sky_mask: torch.Tensor,
max_depth: float = 200.0,
) -> Tuple[torch.Tensor, torch.Tensor]:
"""
Set sky regions to maximum depth and high confidence.
Args:
depth: Depth tensor
depth_conf: Depth confidence tensor
non_sky_mask: Non-sky region mask
max_depth: Maximum depth value for sky regions
Returns:
Tuple of (updated_depth, updated_depth_conf)
"""
depth = depth.clone()
depth_conf = depth_conf.clone()
# Set sky regions to max depth and high confidence
depth[~non_sky_mask] = max_depth
depth_conf[~non_sky_mask] = 1.0
return depth, depth_conf
经过这个流程,原本质量参差不齐的真实世界数据,就被修补和增强了。它们既保留了真实的几何约束,又拥有了由教师模型赋予的丰富细节和完整性。
最后,DA3的最终模型(即学生模型)就在这些高质量的、对齐过的伪标签上进行训练。 这种教师-学生范式,巧妙地绕过了真实世界数据质量差的难题,极大地提升了模型的学习效率和最终性能。
损失函数:
DA3的训练目标函数也经过精心设计,它综合考虑了深度图的准确性、射线图的准确性、最终重建点云的准确性、相机位姿的准确性以及深度图梯度的平滑性,通过多个损失项的加权和,引导模型向着生成高度一致且精确的几何结构的目标优化。
\(\mathcal{L}_T = \alpha \mathcal{L}_{grad} + \mathcal{L}_{gl} + \mathcal{L}_N + \mathcal{L}_{sky} + \mathcal{L}_{obj}\) 其中:
- $\mathcal{L}_{grad}$: 深度图梯度平滑性损失,提升几何准确性;
- $\mathcal{L}_{gl}$: 全局-局部的深度损失,多尺度监督,提高尺度不变性和鲁棒性;
- $\mathcal{L}_N$: 法向量损失,用于约束表面法向量的准确性;
- $\mathcal{L}_{sky}$: 天空区域遮罩损失;
- $\mathcal{L}_{obj}$: 物体区域遮罩损失;
- $\alpha$: 梯度损失的权重系数,值为0.5。
教学单眼模型: 以与教师相同的损失进行学生的监督,这些损失应用在伪深度标签上。仅在教师监督下使用未标记数据进行训练,在标准单眼深度基准测试中达到最先进的性能。
教学度量模型: 应用规范相机空间变换来解决由不同焦距引起的深度模糊问题。为了确保细节清晰,我们采用教师模型的预测作为训练标签。我们将教师模型预测深度的规模和变化与指导所需的真实度量深度标签对齐。用 14 个数据集训练了度量深度模型。
超参数: 使用 AdamW 优化器,并将编码器和解码器的学习率分别设置为 5e-6 和 5e-5。 我们应用随机旋转增强,即以 5% 概率将训练图像以 90 度或 270 度旋转。 把标准焦距 fc 设为 300。我们使用教师对齐预测模型作为监督。 我们以 20% 的概率使用原始的真实化标签进行训练。 batch size 为 64,执行 16 万次迭代。
全新-视觉几何基准
为了更全面、更公平地评估视觉几何估计模型的能力,并推动该领域的持续进步,DA3团队建立了一个全新的、综合性的基准测试。 这个基准不仅评估传统的深度图精度,还直接评估模型预测的相机位姿准确性,以及最终融合生成的3D点云的重建质量。
该基准涵盖了5个多样化的公开数据集,包括HiRoom、ETH3D、DTU、7Scenes、ScanNet++,总计超过89个场景,场景类型从单个物体级别,延伸到复杂的室内房间和广阔的室外环境。
评估流程分为两步:
- 位姿估计评估(Pose estimation): 模型需要处理一个场景中的所有(或最多100张)图像,以纯前馈的方式一次性输出所有相机的位姿,然后与真实的相机位姿进行比较,计算旋转和平移的精度。
- 几何估计评估(Geometry estimation):模型使用自己预测出的位姿和深度图,通过TSDF(截断符号距离函数)融合技术生成三维点云。生成的点云会先与真实的相机位姿进行对齐,然后与真实的场景点云进行比较,计算其准确性(Accuracy)、完整性(Completeness)和F1分数,这些指标能全面地衡量重建质量的好坏。
实验结果令人印象深刻。
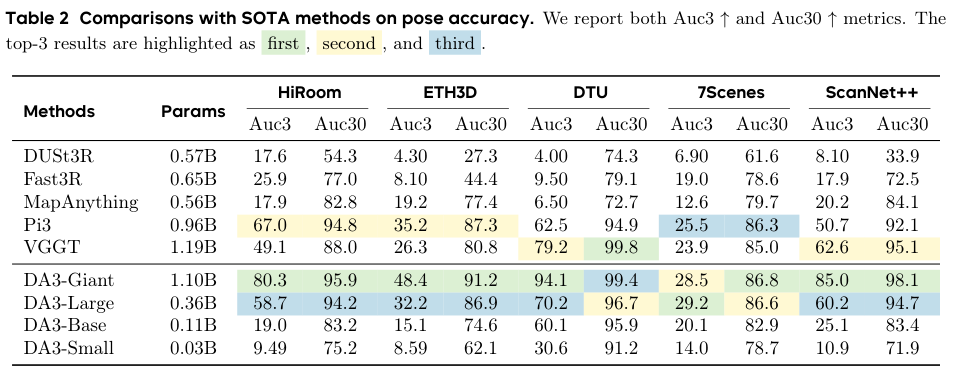
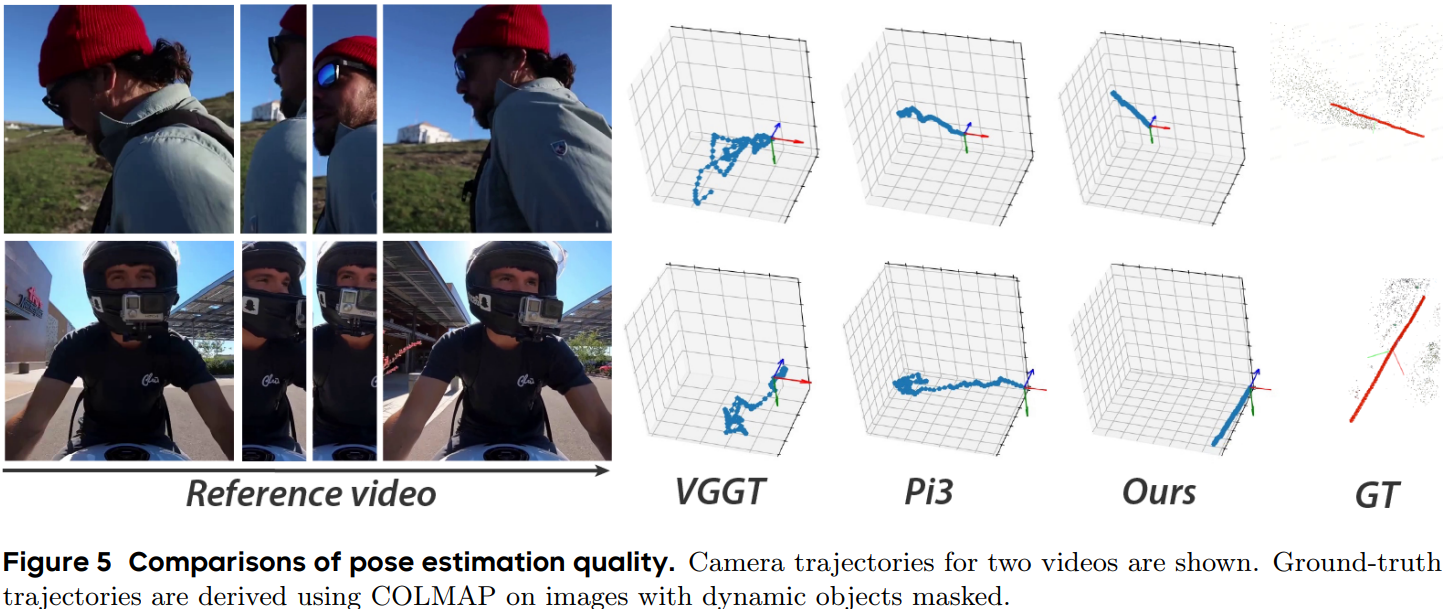

AUC指标: 在评估时,通常会设定一系列的误差阈值(例如,平移误差:5cm, 10cm, 15cm…;旋转误差:1°, 2°, 3°…)。对于每一个阈值,可以计算出预测结果中误差小于该阈值的样本所占的比例。将这个比例作为Y轴,阈值作为X轴,就可以绘制出一条精度曲线。 曲线下面积(AUC,Area Under Curve),曲线下的面积就是AUC。AUC的值越高,说明在所有误差阈值下,模型的整体表现都越好。
在位姿估计方面,DA3-Giant模型(参数量最大的版本)在几乎所有指标上都超越了所有已知的基线方法。 尤其是在要求更严苛的精度阈值下(例如旋转和平移误差小于3度或3%),DA3的领先优势尤为明显,相对于所有竞争者实现了至少8%的相对性能提升。 在ScanNet++这个极具挑战性的数据集上,其相对增益更是高达33%。
在几何估计方面,无论是在位姿未知(pose-free)还是位姿已知(pose-conditioned)的设定下,DA3的表现都堪称统治级。 在所有五个数据集的无位姿设置中,DA3-Giant全面超越了所有对手,刷新了SOTA记录。 更值得注意的是,即使是参数量小得多的DA3-Large版本(0.30B参数,约为Giant版本的三分之一),其性能也极具竞争力,在10个评测设置中的5个上超过了之前的SOTA模型VGGT(1.19B参数)。 这充分证明了DA3架构的卓越效率。
从可视化的结果来看,DA3重建的点云干净、准确、完整,并且保留了非常精细的几何细节,例如物体的纤薄结构和复杂的轮廓,其质量明显优于其他方法。 除了在多视图几何任务上的卓越表现,DA3在传统的单目深度估计基准测试中也展现了最先进的性能,其单目模型在NYUv2、KITTI等经典数据集上的表现优于其前身Depth Anything 2和其他竞争方法。 这证明了DA3的统一框架并未因为追求通用性而牺牲在特定任务上的专精能力。
驱动下游任务
一个强大的基础模型,其价值不仅在于自身性能的卓越,更在于它能作为基石,推动下游相关应用的发展。 DA3团队选择了前馈新视角合成(Feed-Forward Novel View Synthesis, FF-NVS)这一热门且极具挑战性的任务,来展示DA3作为几何基础模型的潜力。 新视角合成的目标是根据一个场景的几张输入图像,合成出任意新视角的图像。
近年来,随着3D高斯散射(3D Gaussian Splatting, 3DGS)技术的兴起,这一领域取得了飞速发展。 3DGS用海量的三维高斯雪花来表示场景,渲染速度快且质量高。 DA3团队遵循其一贯的极简建模策略,在DA3模型的基础上,仅增加了一个额外的DPT头,用于预测与每个像素对齐的3D高斯参数(如不透明度、旋转、缩放和颜色)。
实验:




3DGS 渲染的新视角(32 张图片):





视频重建:DA3 可以从任意数量的视图中恢复视觉空间,涵盖从单视图到多视图的范围。此演示展示了 DA3 从复杂视频中恢复视觉空间的能力。
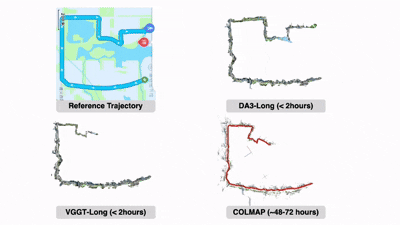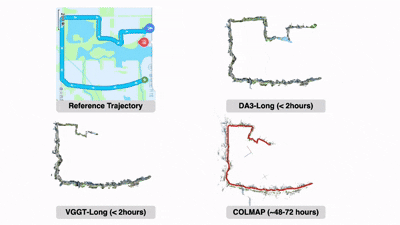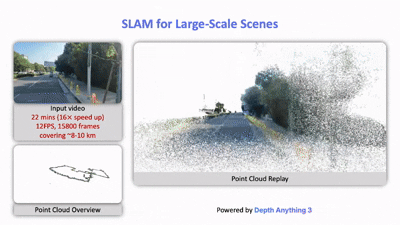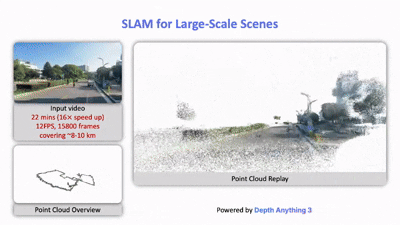
大规模场景的SLAM:精确的视觉几何估计能够提升SLAM的性能。定量结果表明,在大规模环境下,仅用DA3替换VGGT-Long中的VGGT(DA3-Long)就能显著降低漂移,其效果甚至优于需要48小时以上才能完成的COLMAP。
参考资料: https://github.com/ByteDance-Seed/Depth-Anything-3 https://depth-anything-3.github.io/ https://arxiv.org/abs/2511.10647 https://huggingface.co/spaces/depth-anything/depth-anything-3
Depth Anything 3 目前已发布三个系列:主 DA3 系列、单目度量估计系列和单目深度估计系列。嵌套系列:GIANT-LARGE。
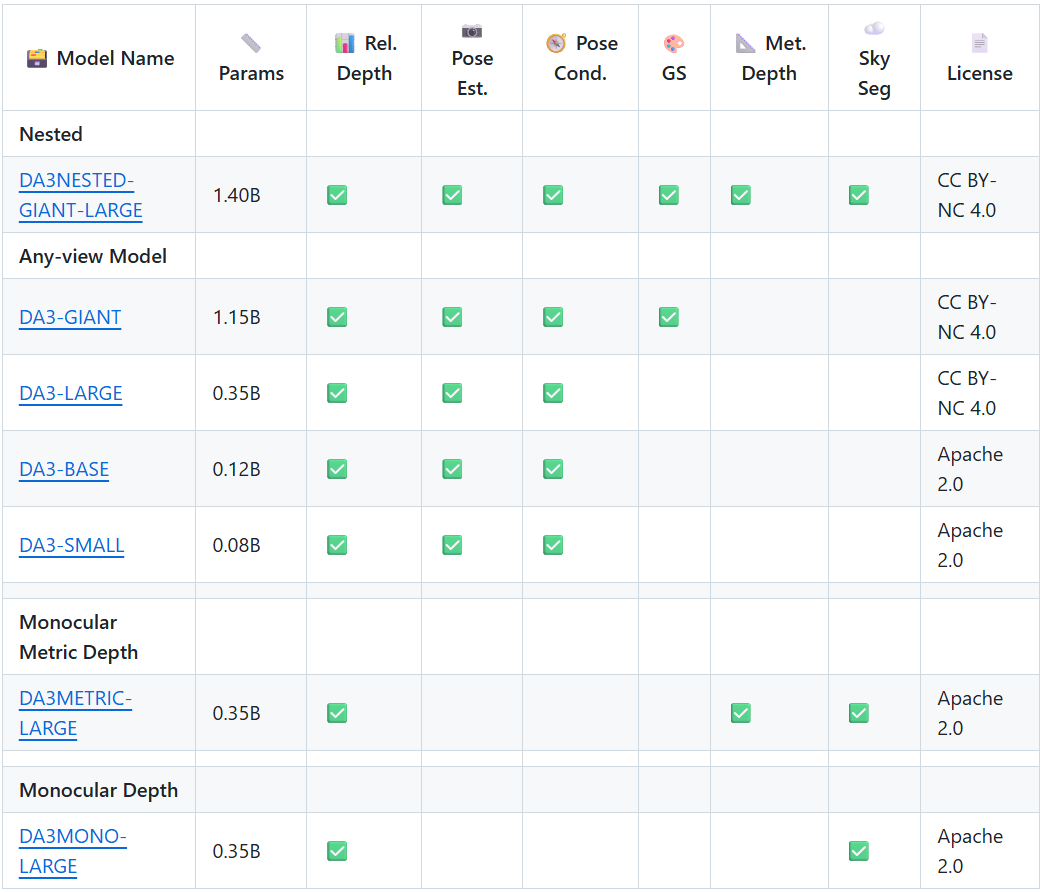
支持多种格式输出:
- GLB: 包含几何和相机的 3D 场景;
- NPZ: 用于研究的数值数据;
- PLY: 点云格式;
- 3DGS 视频: 新视图合成;
- 深度图像: 标准深度图;
模型加载与推理:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import glob, os, torch
from depth_anything_3.api import DepthAnything3
device = torch.device("cuda")
model = DepthAnything3.from_pretrained("depth-anything/DA3NESTED-GIANT-LARGE")
model = model.to(device=device)
# 加载图像
example_path = "assets/examples/SOH"
images = sorted(glob.glob(os.path.join(example_path, "*.png")))
# 运行推理
prediction = model.inference(images)
# 访问结果
print(f"处理后的图像形状: {prediction.processed_images.shape}") # [N, H, W, 3] uint8
print(f"深度图形状: {prediction.depth.shape}") # [N, H, W] float32
print(f"置信度图形状: {prediction.conf.shape}") # [N, H, W] float32
print(f"外参形状: {prediction.extrinsics.shape}") # [N, 3, 4] float32
print(f"内参形状: {prediction.intrinsics.shape}") # [N, 3, 3] float32